Pentagon Math

I don't know about you, but about once every other year, I need to draw a good regular pentagon. Below is a collection of the math I end up re-creating when the need arises.

Final Numbers:

• Internal obtuse angles = 108 degrees
• Vertical Bisector = S * 1.538841
• Dist between side vertices =  S * 1.618034
• Horiz dist to side vertex = S * 0.309017
• Vert dist to side vertex = S * 0.9510565

First, some pentagon basics.

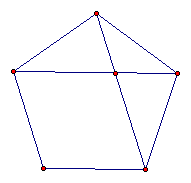
Figure 1: Five Triangles

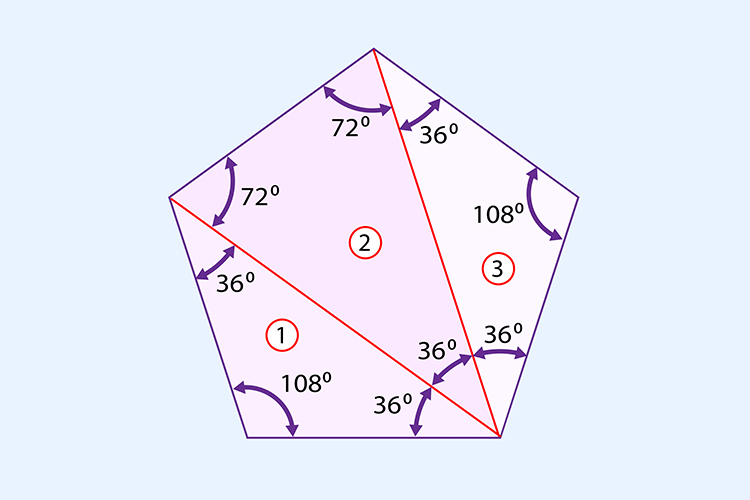Figure 2: A bunch of angles

           

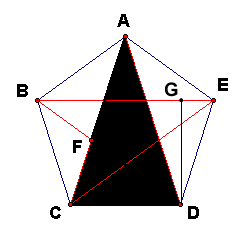Figure 4: Similar Triangles           

Figure 3: Rhombus (equal-sided parallelogram)

Now for some Q&A! The main questions I always have when drawing a regular pentagon are (in relation to the side length): how many degrees are the obtuse inner angles, what is the distance between the side vertices, how long is the vertical bisector, and what are the horizontal and vertical distances from a base vertex to the nearest side vertex?

How many degrees are the obtuse inner angles? 
Figure 1 is the proof I'm usually looking for. I break the pentagon into five triangles sharing the center point as a vertex and with bases of the five sides (as shown). The shared center vertex has 360 degrees split into five angles, so each central angle is 360/5 = 72. Triangles have 180 degrees in their internal angles, so there's 180 - 72 = 108 degrees left. Since the triangles in Figure 1 are isosceles, the two angles made by the pentagon's side are 108/2 = 54. And since I'm usually pretty obtuse, I have to finally convince myself that the two neighboring 54 degree angles of a corner of the pentagon add up to 108 degrees for the internal angles of the pentagon.

What is the distance between the side vertices?
My next question is usually about the horizontal and vertical distances of the side vertices from the base vertices, but I end up having to figure out the distance between the side vertices, as well as the vertical bisector first. Figure 3 and some similar triangles can be used to solve this tricky question.

To start with, Figure 3 shows that the line connecting the side vertices is parallel with the base (this is obvious, but Figure 2 can be used to see it in numbers). Since the pentagon is regular, the same is true if you turn it to make any other side into the base. This means that Figure 3 shows a parallelogram. Opposite sides of a parallelogram must be the same length, otherwise the intersecting lines wouldn't be parallel any more. Therefore, the distance between the side vertices is the side length plus a bit more.

But that bit, tho. We can find it using similar triangles We'll be using the tall black triangle in Figure 4, CAD, and a hard-to-see sideways triangle CDF. Let's call the side length S and the line connecting the bottom right vertex with the top vertex as X. Now for the ratio: S/X = (X-S)/S. First, to explain why S/X (saying "S is to X"); S, the side length of the pentagon, S, is the isosceles arm of the CDF triangle, whereas X is the isosceles arm of the tall CAD triangle. Similarly, X-S represents the little bit we're trying to find, which is the base of the CDF triangle, namely the segment CF. So (X-S)/S is comparing that base to S, the base of CAD, the tall triangle. Now we can solve for X:

S/X = (X-S)/S   (let's get rid of the denominators by multiplying both sides by X and then by S)
S = X*(X-S)/S
S^2 = X*(X-S) = X^2 - SX   (now get everything on one side and use the quadratic formula)
X^2 - SX - S^2 = 0   (quadratic formula: AX^2 + BX + C, X = [-B +- (B^2 - 4AC)^(1/2)] / 2A
X = [S +- (S^2 - 4(1)(-S^2))^(1/2)] / 2 = [S +- (S^2 + 4S^2)^(1/2)] / 2 = [S +- S * 5^(1/2)] / 2
X = S * (1 +- 5^(1/2))/2   (simplified with multiplicative distribution a few times, nothing fancy)

We only care about positive roots of X (it's definitely a positive distance between the side vertices!), so we can ditch the "+-" for just "+". So X, in terms of the side length S, is S * (1 + 5^(1/2)) / 2 = X. The nice thing is, we can just estimate this usually. S times a constant is easy to compute when I definitely need to again in a couple years. Everything in X except this S is (1 + 5^(1/2))/2 = 1.618034 (good enough!).

X = S * 1.618034

How long is the vertical bisector?
The vertical bisector is the vertical line that goes from the top vertex to the middle of the base. Since we have the base, and the hypotenuse (X in our previous derivation), we can use Pythagorean Theorem to solve for the length of the vertical bisector (lets call it H for Height). Normally, we have A^2 + B^2 = C^2, where C is the hypotenuse. Here, we'll have (S/2)^2 + H^2 = X^2. Let's rearrange that since we're solving for H. H^2 = X^2 - (S/2)^2. Below we'll expand X in terms of S and solve for H:

H^2 = X^2 - (S/2)^2   (let's put X in terms of S as we derived above)
H^2 = (S * (1 + 5^(1/2))/2)^2 - (S/2)^2   (now square, use a common denominator, and factor out S)
H^2 = S^2 * (1 + 5^(1/2)^2 / 4 - S^2 / 4 = (S^2 / 4) * [(1 + 5^(1/2))^2 - 1]   (square root time)
H = (S/2) * [(1 + 5^(1/2))^2 - 1]^(1/2)

It's reduce-it-to-a-constant-times-S-time again! Everything except the S in H is:
(1/2) * [(1 + 5^(1/2))^2 - 1]^(1/2) = 1.538841 (come on, I'm not making pentagons that big).

The length of the vertical bisector is: S * 1.538841.

What are the horizontal and vertical distances from a base vertex to the nearest side vertex?
When actually drawing a pentagon, you start with a base, but without a protractor or compass (yes, this all could have just been solved with the angles and a protractor, or a straight edge and compass, but I trust my ability to measure distance better than angles, and I never seem to have those things on hand, and I wouldn't get to do all this fun math ... the list is endless!).

In Figure 4, DG is the vertical distance, and GE is the horizontal distance. We already figured out the length from the black triangle to E along BE as X - S, but here we just need half of it. So GE is
(X - S)/2 = (S * (1 + 5^(1/2))/2 - S)/2 = S * ((1 + 5^(1/2))/2 - 1)/2 = S * ((5^(1/2) - 1)/2)/2
(X - S)/2 = S * (5^(1/2) - 1)/4

Constant time again! (5^(1/2) - 1)/4 = 0.309017

Now for the vertical distance, which I'll call V. Pythagoras don't fail me now! (using the triangle DGE, of course)

V^2 = S^2 - [S * (5^(1/2) - 1)/4]^2 = S^2 - S^2 * ((5^(1/2) - 1)/4)^2 = S^2 * [1 - ((5^(1/2) - 1)/4)^2]
V = S * [1 - ((5^(1/2) - 1)/4)^2]^(1/2)

Well that just begs for a constant! [1 - ((5^(1/2) - 1)/4)^2]^(1/2) = 0.9510565

Final Numbers:

• Internal obtuse angles = 108 degrees
• Vertical Bisector = S * 1.538841
• Dist between side vertices =  S * 1.618034
• Horiz dist to side vertex = S * 0.309017
• Vert dist to side vertex = S * 0.9510565

Final note: I noticed that ((5^(1/2) - 1)/4 = 1/(5^(1/2) + 1), which makes sense if you use the pattern A^2 - B^2 = (A+B)(A-B)

Infinities part 2: Cantor's Diagonalization Theorem

Check out Infinities part 1 for some background. Now you know what countable infinity is, but what about uncountable infinity? Why is it bigger, what can't you count, and who is this Cantor fellow anyways?

Georg Cantor was one of the great mathematicians. He invented set theory (which all modern math is based on), showed the world an infinity of infinities, and became increasingly insane.

Now, on to the theorem. I didn't get this theorem the first time I heard it. Or the second. Or for a few years of hearing it. I had to really think about it before I understood what was going on. I'll try to include all of those little intuitive leaps that no one tells you about, but that you need to make in order to really understand why it works. The theorem states that the Real numbers are "more numerous" than the counting numbers. Clearly both are infinite, but the Real infinity is larger than the countable infinity. I will prove that the Real numbers between 0 and 1 are "more numerous" than the counting numbers. If that set is uncountable, then the entire set of the Real numbers must be at least that big and thus uncountable as well. It is more difficult to prove that the Real numbers and the Real numbers between 0 and 1 are the same infinite size. It is also more difficult to prove that the Real plane is yet a bigger infinity than the Real number line, but that is a post for another time (although probably not, because this post is the most interesting part).

Outline:

• Come up with an arbitrary way of counting the Real numbers between 0 and 1. By arbitrary, I don't mean a particular way chosen at random. Instead, arbitrary means a way that encompasses all possible ways. There isn't a way to count them that isn't covered by this arbitrary method.
• Show that the arbitrary method misses a Real number. This missed number is constructed out of the arbitrary counting method, so you can't just add it to the counting method and try again.
• Following the unique pairing idea in Infinities part 1, show that there is no counting number pair for the missed Real number.

The biggest problem that I had with this was the arbitrary counting method. I didn't believe that it really took care of all of the possible ways that you could order and count the Real numbers. Heck, the proof that the rational numbers are countable requires a pretty clever ordering and counting method, so why couldn't that exist here?! Let's look at the arbitrary counting method.

Every Real number between 0 and 1 can be written as an infinite decimal number: 0.1232454729063373.... In some cases, like with 1/2 or .5, we can write it as 0.5000000.... I will introduce a little notation in order to describe the counting method. Consider one of these infinite decimals which we'll refer to as d1 (read dee one). We're going to want to refer to specific digits of each number that we count, so we'll say that d1 = d11d12d13d14d15.... Suppose d1 is pi/10 (0.31415926....) Then d11 is 3, d12 is 1, d13 is 4, d14 is 1, and so on. Our next number would be d2 = d21d22d23d24d25.... We end up with a matrix:

d1 = 0.d11d12d13d14....

d2 = 0.d21d22d23d24....

d3 = 0.d31d32d33d34....

...

dn = 0.dn1dn2dn3...dnn....

This counting method is arbitrary. Whatever counting method is chosen, there will be a d1, a d2, and so on. This matrix represents any possible counting method since it doesn't state what the ordered numbers are. It allows you to fill in the d's with whatever counting system you want to try. This is the tricky part. If you don't believe that this represents any possible counting of the Real numbers from 0 to 1, then you won't believe the rest of the proof, so I'll rephrase the point. The way that you show that an infinite set is countable (like with the integers or the rationals) is to create a unique pair for every element of the two sets. Thus, you have to pair 1 with something, 2 with something else, 3 with something else, and so on. Moreover, you can't miss any elements of the set you are trying to count. When pairing the counting numbers to the integers, you could choose a way that works, but you could also choose a way that doesn't. The way that works is to oscillate between positive and negative numbers in order to cover the entire set of integers with the counting numbers. A counting method that wouldn't work is if you just matched 1:1, 2:2, 3:3, and so on. You would miss all of the negative numbers! What we are proving with this matrix is not just why a particular counting method doesn't work, like matching 1:1, 2:2, and so on, but why ANY counting method doesn't work. By not putting actual numbers in for d1, d2, etc., we have allowed any pairing of 1:d1, 2:d2, 3:d3, .... No matter how clever you can get, you will still have to match 1 with something. d1 is a placeholder for that something. d2 is the placeholder for what you match 2 with, and so on. If you don't get this yet, don't feel bad. This is the hard part of the proof.

Whatever numbers you would choose for each d of this counting method, you would always miss at least one Real number between 0 and 1. Let's construct this number; we'll call it c. The digits of c are chosen based on the digits of the d's. c is going to be an infinitely long decimal, and we'll denote it as c = c1c2c3c4.... Here's where the diagonalization comes in to play: choose c1 to be any number between 0 and 9 except whatever d11 is. c2 will be between 0 and 9, but different from d22. c3 is between 0 and 9, but different from d33. In other words, if you take that matrix of d's above and create a number, call it b, by drawing a diagonal line from the top left to the bottom right, each digit you hit in the matrix becomes the next digit of b; b = d11d22d33d44d55.... The c number is different from the b number at every digit. We have created this c number very specifically so that it doesn't exist as any d. By being different from the diagonal AT EVERY DIGIT, the c number can't be one of the d numbers. Consider d7. c is not d7, since d7 = 0.d71d72d73d74d75d76d77.... but c = c1c2c3c4c5c6c7.... where c7 is different from d77. Consider d2. d2 = 0.d21d22d23.... but c = c1c2c3.... where c2 is different from d22. You can see that for any d, there will be a digit of the c number that will be in the same location but different in value from the d number. Thus the c number isn't any of the d numbers!

c is a real number between 0 and 1 that falls outside of any given counting method. Notice the word given. I'm saying that once a counting method is chosen, whichever one it is, it will miss at least one number. Adding that one number to the counting method doesn't fix this, because by modifying the d's with the new number, you modify the diagonal and thus the missed number. The number c that is left out depends on the counting method. Whatever counting method is chosen, this c number will exist and it won't be counted. You can't come up with some super-clever counting method that beats this, because whatever that counting method is, there will be a c number that crops up which isn't covered.

I will finish with some intuition. The Real numbers consist only of rational and irrational numbers. We know that the rational numbers are countable, so it is the irrational numbers that are uncountably infinite. Somehow, the irrational numbers are "more numerous" than the rationals. The intuition that helps here is that irrational numbers all end in non-repeating infinite decimals. Rational numbers either end, or end in repeating infinite decimals. The amount of "information" in an irrational number is infinite, while in a rational number it is finite. The rationals are an infinite set of finites, while the irrationals are an infinite set of infinites.

Infinities

Most people think about Infinity as being the biggest number, but I'm here to tell you that you're wrong on both accounts! First, there are different "sizes" of infinities, and second, infinity is not a number at all.

If infinity was a number, then basic algebraic principles would hold true for it:
 + 1 =  (we all know that infinity plus one is still infinity, but what if we subtract  from both sides?)
 + 1 -  =  - 
1 = 0

If infinity is a number, then 1=0. I'm going to go ahead and say that infinity is not a number. What is a number, then? That's another post related to field axioms. We're talking about infinities.

My favorite puzzle that hints at the difference between infinite whole numbers and infinite Real numbers is as follows:

Suppose you travel along the edges of a square, with edge lengths of 1 mile, from one corner to the opposite corner (image 1). You will clearly have to travel 2 miles. Suppose you quarter the square and then walk down a half mile, towards the center a half mile, down a half mile, and over to the opposite corner the last half mile (image 2). You will still have walked 2 miles. Quarter it again and follow the pattern (image 3). You will continue to walk 2 miles every time.

Do this process over and over again, and you will always be walking two miles (ignore reality as far as considering how pivoting and turning affects walking, we're really just talking about the distance of the path). What happens to this situation as the number of quarterings approaches infinity? It looks like the shape of the path will become the diagonal line between the opposite corners of the square. However, the length of the path is always 2 miles. The act of quartering it again doesn't modify the distance, no matter how many times you do it.

The diagonal of a square is NOT twice the side length. That would be an interesting universe, but it is not our own. In fact, the diagonal of a square is the square root of 2 times the side length. A little pythagorean theorem gets you there. Consider a square with a side length of x (x can be 5, pi, or whatever). Pythagorean theorem tells us that the square of the hypotenuse of any right triangle is the sum of the squares of its sides, or as you may have commonly seen a^2 + b^2 = c^2. The ^ sign means "to the power," so 3^2 is 3*3 = 9. In our right triangle, made out of two sides of a square and the diagonal that connects them, we have x as the value for a and b in the pythagorean theorem and c is the length of the diagonal. So: x^2 + x^2 = c^2. We can add the two x^2 to get 2*(x^2) = c^2. By taking the square root of both sides, we get c = (2^(1/2))*x, or written out: the length of the diagonal of a square is equal to the square root of two times the length of the square's sides.

Traveling down the diagonal, we go 2^(1/2) miles, but traveling down the infinitely jagged diagonal by way of quartering is 2 miles. Why doesn't our quartering attempt give us a diagonal line, EVEN WHEN WE DO IT AN INFINITE NUMBER OF TIMES!? We can't do it any more! Jeez!

The truth is startling. There are different 'sizes' or 'levels' of infinity. The good news is that there are better comebacks than "infinity plus one!" Before I explain anything else, I will state what we know and what we think about infinities. The counting numbers (1, 2, 3, ....), the integers (...., -2, -1, 0, 1, 2, ....), and the rational numbers or fractions (3/17, -19/4324, 0, etc.) are all infinitely large sets, and that infinity is the same. It's called countably infinite. Our process of quartering was a countably infinite process. The real numbers (0, 31/5, pi, 2^(1/2), and many more) is uncountably infinite (which really means bigger than countable infinity). If you think about the real numbers as lying on the real number line, then the real number plane (x-y axis) is yet a larger infinity than the real number line. The real space, which is 3-dimensions of the real number line is bigger than the real plane. Each higher dimension of real space (hyperspace really) is a bigger infinity than the last. That's what we know. What we suspect, is that we have determined all sizes of infinity. They start at countable infinity and travel up the dimensions of the real numbers. This is just a hypothesis. It could be that there are infinities between the real number line and the real plane, but no one has been able to prove that claim true or false.

In the rest of this post, I will lay out the proof that the counting numbers, the integers, and the rational numbers are all of the same size of infinity. I will not prove that the real numbers are larger because it is a really hard proof to follow and would take up too much space and time here to be useful. That will be another post about The Cantor Diagonalization Theorem.

We can say that two sets, even two infinitely large sets, are the same size if we can pair up all of their elements without leaving any out. For instance, {1,3,5,7} is the same size as {2,4,6,8} because we can pair up 1:2, 3:4, 5:6, and 7:8 (the order doesn't matter; we could have paired 1:4, 5:2, ...). We can also do this for the counting numbers and the integers. Basically, pair up the even counting numbers with the positive integers and the odd counting numbers with the negative integers. Also, pair 2 with 0 for simplicity. The pairings go 1:-1, 2:0, 3:-2, 4:1, 5:-3, 6:2, etc. The idea is that I can give you the counting pair to any integer that you give to me, and the integer to any counting number. Thus, every integer and counting number has a unique pair. If I can count the integers, then there aren't any more integers than there are counting numbers.

Rational numbers are a little more difficult. Fractions are all of the form a/b or -a/b, where a and b are counting numbers. In order to pair up the counting numbers to the rational numbers, we can create a matrix (not The Matrix, don't worry) and count the elements in a diagonal fashion.

We pair up the counting numbers and fractions in the following way: 1:1/1, 2:1/2, 3:2/1, 4:1/3, 5:2/2, 6:3/1, 7:1/4, 8:2/3, etc. We are following the blue lines starting with the one that goes through 1/1 from bottom left to top right and then jumping back down to the bottom left of the next line to the right. In this way we can count all of the positive rational numbers. It's a short intuitive leap to create a matrix of the negative rational numbers and count them all.


It would seem like there would be more integers, and certainly more rational numbers, than there are counting numbers, but there really aren't. With finite sets, when one set contains another set and has additional elements that the other doesn't, it is bigger. But with infinite sets, it's not that simple.

Repeating Decimals

Question
Occasionally I need to represent a repeating decimal, such as .11111..., .523523523..., or even 3.0714256425642564256..., as a fraction for simplification or number theoretic purposes, or just because I feel like it. What algorithm allows us to do this conversion?

Math Time
Here's an outline for what we're going to do:

1. First we are going to ignore the non-repeating part. We'll deal with it later. We will just pretend that we have 0.523523523..., or whatever the repeating part is (left justified up to the decimal point).
2. Next we're going to look at the repeating decimal as similar chunks added together which have increasing powers of 10 in the denominator.
3. After factoring out the similar numerators, we will approach the sum of reciprocal powers of 10 and notice that they sum to a fraction similar to 1/9999..., depending on how long the repeating part of the decimal is.
4. Finally we'll add back in the non-repeating part to complete the fractional representation.

By showing this algorithm for any arbitrary repeating decimal, you must realize that, unlike the irrational square root of 2, all repeating decimals are rational! Now, on to the proof!

For notation, I will use y1y2...ym to refer to the m digits of the non-repeating part and x1x2x3...xn to refer to the n digits of the repeating part. An arbitrary digit of the non-repeating part will be referred to as yi, and of the repeating part as xi.

First, let us remove the non-repeating part. Let R be the number with a repeating decimal. R = y1y2...ymx1x2...xn. Even if the repeating begins to the left of the decimal place, count everything to the left of the decimal place as being part of the non-repeating part. Thus, all xi occur to the right of the decimal point. Moreover, multiply R by one (while multiplying by 1 doesn't change anything, it sure can be useful!) in the form of 10^k / 10^k where k is the number of decimal places that the yi go to the right of the decimal point (3.07123123123... would require k=2 since the non-repeating part, 3.07, goes 2 places to the right of the decimal point). If we hold 1/10^k as a multiplied factor to the left of the equaiton and multiply in 10^k, then this will cause the decimal place to lie directly between the yi and xi. So R = 1/10^k (y1y2...ym . x1x2...xn....) = 1/10^k (y1y2...ym + .x1x2...xn...). Notice the . used to show where the decimal point is located. Now let's focus on the xi.

Notice that .x1x2...xnx1x2...xnx1x2...xn.... can be split up into an infinite sum, namely x1x2...xn / 10^n + x1x2...xn / 10^2n + x1x2...xn / 10^3n + .... (if we had .454545.... we would get 45/100 + 45/10000 + 45/1000000 + ....). Factor out x1x2...xn and you are left with x1x2...xn (10^-n + 10^-2n + 10^-3n + ....). Time to examine that sum of spaced out reciprocal powers of 10.

First, notice that .111111...., or 1/10 + 1/100 + 1/1000 + ...., is 1/9. This is trivial using long division. Let's look at .01010101.... now. A little insight shows us that it is 1/99. If we continue in this fashion, we see that .001001001.... is 1/999, and so on. In other words, the infinite sum 10^-n + 10^-2n + 10^-3n + .... = 1/999.... that is, 1 over n 9's. Let's put that finding back into our problem. (For brevity, I avoided proving this step, but it is commonly called a geometric series and is cleverly proven using the idea of telescoping).

So we have x1x2...xn (10^-n + 10^-2n + ....) = x1x2...xn (1/9999...). Remembering about our 10^k / 10^k trick earlier, R = 1/10^k (y1y2...ym + x1x2...xn / 999...). Using basic fraction arithmetic (multiply each fraction by the number one in the form of D/D where D is the denominator of the other fraction involved) we get R =  ((999...) * y1y2...ym + x1x2...xn) / (999... * 10^k), where 999... is the number of 9's equal to the length of the repeating part, or n 9's.

As an example, let's take a fraction with 7 in the denominator, which, other than numerators that are divisible by 7, always ends up as a repeating decimal. 17/7 = 2.428571428571.... Using our tricks (note, we don't have to do our 10^k trick) we get (999999*2 + 428571) / 999999 which, surprisingly enough, is 2428569 / 999999 = (142857/142857) * (17/7) = 2.428571428571.... and so on. Amazing!

Final Answers
In order to turn a number with a repeating decimal into a fraction, first determine where the decimal place "should" go. Take the number digits in the non-repeating portion to the right of the decimal point (2 for 3.07666666...) and replace k below with that number. Figure out the length of the repeating portion (only consider the repeating portion to the right of the decimal place, 1231.231231.... would have a repeating length of 3 and we would consider the repeating portion to be 231). There will be a term of 9999... where the number of 9s is the same as the length of the repeating portion.

So for a number with a repeating decimal, it is equal to the fraction [9999... * (the non-repeating portion as a whole number) + (the repeating portion as a whole number)] / (9999... * 10^k)

Or if you followed along above it is [(999...) * y1y2...ym + x1x2...xn] / (999... * 10^k)

A few more examples:

• 3.04123123123... becomes (999 * 304 + 123) / (999 * 100) = 303819 / 99900 = 3/3 * 101273 / 33300
• 12341.234123412341... becomes (9999 * 12341 + 2341) / (9999) = 123400000 / 9999 (that's the reduced form!)
• .0000354235423542.... becomes (9999*0 + 3542) / (9999 * 10000) = 3542 / 99990000 = 22/22 * 161/ 4545000
• 17.363636.... becomes (99*17 + 36) / 99 = 1719 / 99 = 9/9 * 191 / 11

If you're curious how I'm finding the common factor of 3/3, 22/22, and 9/9 in the examples above, I'm just finding the Greatest Common Divisor (gcd) of the numerator and denominator. Some number theory is required to understand how to do that (Euclidean Algorithm is easy and fast, but is a little magical without really thinking about it). I just used a gcd calculator online.