If infinity was a number, then basic algebraic principles would hold true for it:
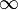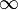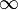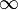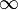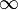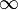
+ 1 = (we all know that infinity plus one is still infinity, but what if we subtract from both sides?) + 1 - = - 1 = 0
If infinity is a number, then 1=0. I'm going to go ahead and say that infinity is not a number. What is a number, then? That's another post related to field axioms. We're talking about infinities.
My favorite puzzle that hints at the difference between infinite whole numbers and infinite Real numbers is as follows:
Suppose you travel along the edges of a square, with edge lengths of 1 mile, from one corner to the opposite corner (image 1). You will clearly have to travel 2 miles. Suppose you quarter the square and then walk down a half mile, towards the center a half mile, down a half mile, and over to the opposite corner the last half mile (image 2). You will still have walked 2 miles. Quarter it again and follow the pattern (image 3). You will continue to walk 2 miles every time.
Do this process over and over again, and you will always be walking two miles (ignore reality as far as considering how pivoting and turning affects walking, we're really just talking about the distance of the path). What happens to this situation as the number of quarterings approaches infinity? It looks like the shape of the path will become the diagonal line between the opposite corners of the square. However, the length of the path is always 2 miles. The act of quartering it again doesn't modify the distance, no matter how many times you do it.
The diagonal of a square is NOT twice the side length. That would be an interesting universe, but it is not our own. In fact, the diagonal of a square is the square root of 2 times the side length. A little pythagorean theorem gets you there. Consider a square with a side length of x (x can be 5, pi, or whatever). Pythagorean theorem tells us that the square of the hypotenuse of any right triangle is the sum of the squares of its sides, or as you may have commonly seen a^2 + b^2 = c^2. The ^ sign means "to the power," so 3^2 is 3*3 = 9. In our right triangle, made out of two sides of a square and the diagonal that connects them, we have x as the value for a and b in the pythagorean theorem and c is the length of the diagonal. So: x^2 + x^2 = c^2. We can add the two x^2 to get 2*(x^2) = c^2. By taking the square root of both sides, we get c = (2^(1/2))*x, or written out: the length of the diagonal of a square is equal to the square root of two times the length of the square's sides.
Traveling down the diagonal, we go 2^(1/2) miles, but traveling down the infinitely jagged diagonal by way of quartering is 2 miles. Why doesn't our quartering attempt give us a diagonal line, EVEN WHEN WE DO IT AN INFINITE NUMBER OF TIMES!? We can't do it any more! Jeez!
The truth is startling. There are different 'sizes' or 'levels' of infinity. The good news is that there are better comebacks than "infinity plus one!" Before I explain anything else, I will state what we know and what we think about infinities. The counting numbers (1, 2, 3, ....), the integers (...., -2, -1, 0, 1, 2, ....), and the rational numbers or fractions (3/17, -19/4324, 0, etc.) are all infinitely large sets, and that infinity is the same. It's called countably infinite. Our process of quartering was a countably infinite process. The real numbers (0, 31/5, pi, 2^(1/2), and many more) is uncountably infinite (which really means bigger than countable infinity). If you think about the real numbers as lying on the real number line, then the real number plane (x-y axis) is yet a larger infinity than the real number line. The real space, which is 3-dimensions of the real number line is bigger than the real plane. Each higher dimension of real space (hyperspace really) is a bigger infinity than the last. That's what we know. What we suspect, is that we have determined all sizes of infinity. They start at countable infinity and travel up the dimensions of the real numbers. This is just a hypothesis. It could be that there are infinities between the real number line and the real plane, but no one has been able to prove that claim true or false.
In the rest of this post, I will lay out the proof that the counting numbers, the integers, and the rational numbers are all of the same size of infinity. I will not prove that the real numbers are larger because it is a really hard proof to follow and would take up too much space and time here to be useful. That will be another post about The Cantor Diagonalization Theorem.
We can say that two sets, even two infinitely large sets, are the same size if we can pair up all of their elements without leaving any out. For instance, {1,3,5,7} is the same size as {2,4,6,8} because we can pair up 1:2, 3:4, 5:6, and 7:8 (the order doesn't matter; we could have paired 1:4, 5:2, ...). We can also do this for the counting numbers and the integers. Basically, pair up the even counting numbers with the positive integers and the odd counting numbers with the negative integers. Also, pair 2 with 0 for simplicity. The pairings go 1:-1, 2:0, 3:-2, 4:1, 5:-3, 6:2, etc. The idea is that I can give you the counting pair to any integer that you give to me, and the integer to any counting number. Thus, every integer and counting number has a unique pair. If I can count the integers, then there aren't any more integers than there are counting numbers.
Rational numbers are a little more difficult. Fractions are all of the form a/b or -a/b, where a and b are counting numbers. In order to pair up the counting numbers to the rational numbers, we can create a matrix (not The Matrix, don't worry) and count the elements in a diagonal fashion.
We pair up the counting numbers and fractions in the following way: 1:1/1, 2:1/2, 3:2/1, 4:1/3, 5:2/2, 6:3/1, 7:1/4, 8:2/3, etc. We are following the blue lines starting with the one that goes through 1/1 from bottom left to top right and then jumping back down to the bottom left of the next line to the right. In this way we can count all of the positive rational numbers. It's a short intuitive leap to create a matrix of the negative rational numbers and count them all.
It would seem like there would be more integers, and certainly more rational numbers, than there are counting numbers, but there really aren't. With finite sets, when one set contains another set and has additional elements that the other doesn't, it is bigger. But with infinite sets, it's not that simple.
I stumbled across this blog while I was taking a look at other sites that talked about the Cantor Diagonalization proof; overall I like it. Here's something that you might like:
ReplyDeleteIn this post you talk about N-dimensional figures using real numbers (real line, real plane, etc), and say that these systems form the tower of increasing cardinal numbers. Actually, you can show that any two N-dimensional shapes have a bijection to each other, and thus are at the same "level" of infinity. The key step is a map to the real interval [0, 1) from an N-dimensional interval where each coordinate is between 0 and 1. You take the coordinates (a1, a2, ... aN) of an N-dimensional point a and assign them to a single point b on the real line like so:
b = 0.a1(1)a2(1)...aN(1)a1(2)a2(2)....
Where a1(1) means the first decimal digit of a1. This is completely discontinuous of course, and the completed process requires a bit more massaging of corner cases and transformations than is appropriate for a blog comment. The good news of this is that the "higher" infinities are even cooler and more mysterious than an N-dimensional extension of the reals.
Anyway I hope you keep this site up; it's good to see another fledgling, fun math blog out there.
You say that "The real space, which is 3-dimensions of the real number line is bigger than the real plane. Each higher dimension of real space (hyperspace really) is a bigger infinity than the last. That's what we know."
ReplyDeleteBut could you illustrate this?