Final Numbers:
- Internal obtuse angles = 108 degrees
- Vertical Bisector = S * 1.538841
- Dist between side vertices = S * 1.618034
- Horiz dist to side vertex = S * 0.309017
- Vert dist to side vertex = S * 0.9510565
First, some pentagon basics.
 |
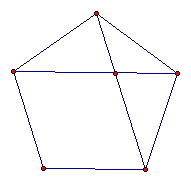
| Figure 1: Five Triangles |
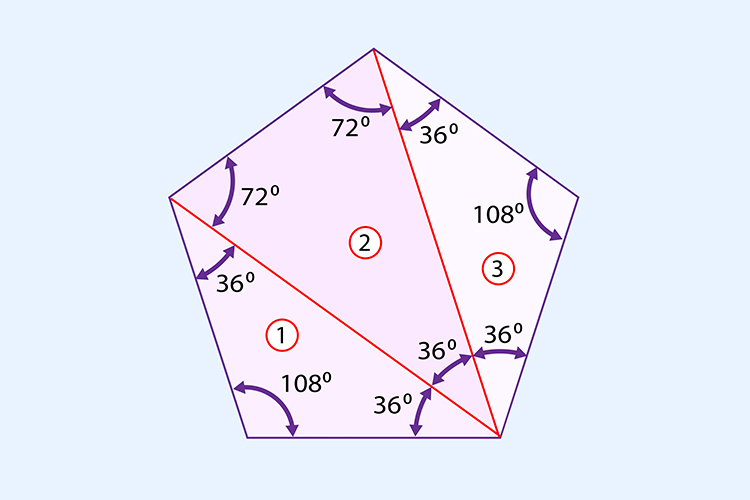 |
| Figure 2: A bunch of angles |
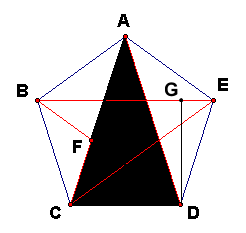 |
| Figure 4: Similar Triangles |
 |
| Figure 3: Rhombus (equal-sided parallelogram) |
Now for some Q&A! The main questions I always have when drawing a regular pentagon are (in relation to the side length): how many degrees are the obtuse inner angles, what is the distance between the side vertices, how long is the vertical bisector, and what are the horizontal and vertical distances from a base vertex to the nearest side vertex?
How many degrees are the obtuse inner angles?
Figure 1 is the proof I'm usually looking for. I break the pentagon into five triangles sharing the center point as a vertex and with bases of the five sides (as shown). The shared center vertex has 360 degrees split into five angles, so each central angle is 360/5 = 72. Triangles have 180 degrees in their internal angles, so there's 180 - 72 = 108 degrees left. Since the triangles in Figure 1 are isosceles, the two angles made by the pentagon's side are 108/2 = 54. And since I'm usually pretty obtuse, I have to finally convince myself that the two neighboring 54 degree angles of a corner of the pentagon add up to 108 degrees for the internal angles of the pentagon.
What is the distance between the side vertices?
My next question is usually about the horizontal and vertical distances of the side vertices from the base vertices, but I end up having to figure out the distance between the side vertices, as well as the vertical bisector first. Figure 3 and some similar triangles can be used to solve this tricky question.
To start with, Figure 3 shows that the line connecting the side vertices is parallel with the base (this is obvious, but Figure 2 can be used to see it in numbers). Since the pentagon is regular, the same is true if you turn it to make any other side into the base. This means that Figure 3 shows a parallelogram. Opposite sides of a parallelogram must be the same length, otherwise the intersecting lines wouldn't be parallel any more. Therefore, the distance between the side vertices is the side length plus a bit more.
But that bit, tho. We can find it using similar triangles We'll be using the tall black triangle in Figure 4, CAD, and a hard-to-see sideways triangle CDF. Let's call the side length S and the line connecting the bottom right vertex with the top vertex as X. Now for the ratio: S/X = (X-S)/S. First, to explain why S/X (saying "S is to X"); S, the side length of the pentagon, S, is the isosceles arm of the CDF triangle, whereas X is the isosceles arm of the tall CAD triangle. Similarly, X-S represents the little bit we're trying to find, which is the base of the CDF triangle, namely the segment CF. So (X-S)/S is comparing that base to S, the base of CAD, the tall triangle. Now we can solve for X:
S/X = (X-S)/S (let's get rid of the denominators by multiplying both sides by X and then by S)
S = X*(X-S)/S
S^2 = X*(X-S) = X^2 - SX (now get everything on one side and use the quadratic formula)
X^2 - SX - S^2 = 0 (quadratic formula: AX^2 + BX + C, X = [-B +- (B^2 - 4AC)^(1/2)] / 2A
X = [S +- (S^2 - 4(1)(-S^2))^(1/2)] / 2 = [S +- (S^2 + 4S^2)^(1/2)] / 2 = [S +- S * 5^(1/2)] / 2
X = S * (1 +- 5^(1/2))/2 (simplified with multiplicative distribution a few times, nothing fancy)
We only care about positive roots of X (it's definitely a positive distance between the side vertices!), so we can ditch the "+-" for just "+". So X, in terms of the side length S, is S * (1 + 5^(1/2)) / 2 = X. The nice thing is, we can just estimate this usually. S times a constant is easy to compute when I definitely need to again in a couple years. Everything in X except this S is (1 + 5^(1/2))/2 = 1.618034 (good enough!).
X = S * 1.618034
How long is the vertical bisector?
The vertical bisector is the vertical line that goes from the top vertex to the middle of the base. Since we have the base, and the hypotenuse (X in our previous derivation), we can use Pythagorean Theorem to solve for the length of the vertical bisector (lets call it H for Height). Normally, we have A^2 + B^2 = C^2, where C is the hypotenuse. Here, we'll have (S/2)^2 + H^2 = X^2. Let's rearrange that since we're solving for H. H^2 = X^2 - (S/2)^2. Below we'll expand X in terms of S and solve for H:
H^2 = X^2 - (S/2)^2 (let's put X in terms of S as we derived above)
H^2 = (S * (1 + 5^(1/2))/2)^2 - (S/2)^2 (now square, use a common denominator, and factor out S)
H^2 = S^2 * (1 + 5^(1/2)^2 / 4 - S^2 / 4 = (S^2 / 4) * [(1 + 5^(1/2))^2 - 1] (square root time)
H = (S/2) * [(1 + 5^(1/2))^2 - 1]^(1/2)
It's reduce-it-to-a-constant-times-S-time again! Everything except the S in H is:
(1/2) * [(1 + 5^(1/2))^2 - 1]^(1/2) = 1.538841 (come on, I'm not making pentagons that big).
The length of the vertical bisector is: S * 1.538841.
What are the horizontal and vertical distances from a base vertex to the nearest side vertex?
When actually drawing a pentagon, you start with a base, but without a protractor or compass (yes, this all could have just been solved with the angles and a protractor, or a straight edge and compass, but I trust my ability to measure distance better than angles, and I never seem to have those things on hand, and I wouldn't get to do all this fun math ... the list is endless!).
In Figure 4, DG is the vertical distance, and GE is the horizontal distance. We already figured out the length from the black triangle to E along BE as X - S, but here we just need half of it. So GE is
(X - S)/2 = (S * (1 + 5^(1/2))/2 - S)/2 = S * ((1 + 5^(1/2))/2 - 1)/2 = S * ((5^(1/2) - 1)/2)/2
(X - S)/2 = S * (5^(1/2) - 1)/4
Constant time again! (5^(1/2) - 1)/4 = 0.309017
Now for the vertical distance, which I'll call V. Pythagoras don't fail me now! (using the triangle DGE, of course)
V^2 = S^2 - [S * (5^(1/2) - 1)/4]^2 = S^2 - S^2 * ((5^(1/2) - 1)/4)^2 = S^2 * [1 - ((5^(1/2) - 1)/4)^2]
V = S * [1 - ((5^(1/2) - 1)/4)^2]^(1/2)
Well that just begs for a constant! [1 - ((5^(1/2) - 1)/4)^2]^(1/2) = 0.9510565
Final Numbers:
- Internal obtuse angles = 108 degrees
- Vertical Bisector = S * 1.538841
- Dist between side vertices = S * 1.618034
- Horiz dist to side vertex = S * 0.309017
- Vert dist to side vertex = S * 0.9510565
Final note: I noticed that ((5^(1/2) - 1)/4 = 1/(5^(1/2) + 1), which makes sense if you use the pattern A^2 - B^2 = (A+B)(A-B)
